概要
地球の位置を指し示すための指標として、緯度・経度という指標があることはご存知かと思います。地図を見る際に役立つのはもちろん、「緯度・経度の組」が2つあれば、その間の距離を計算することもできます。
ですが、その距離をどのように計算すればよいかはご存知でしょうか。この記事では、計算手順に関する概要をまとめた後、この用途に使えるライブラリを例示していきます。
地球は丸くない
この話をすると、「地球」というぐらいだし三角関数で求まるのでは……と考えた人はいるかもしれません。実際、球面における2点間の距離は、「球面三角法」という技術を使って求めることができます。
しかし、現実の地球は「真球」と呼ぶにはちょっといびつです。山や谷があるから……というだけでなく、「平均的な海面の高さ (ジオイド面)」からして、遠心力の影響で赤道方向にちょっとだけ膨らんでいるからです。
そのため、「地球楕円体」と呼ばれる形状……例えるならミカンやラグビーボールのような形……を「地球の形」として計算するのが主流となっています。例えば「WGS84」という、GPS にも使用される一般的な地球楕円体はこんな感じ。
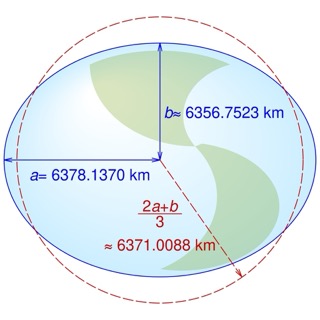
(出典:Cmglee, CC BY-SA 4.0, ウィキメディア・コモンズ)
距離を計算するには?
地球楕円体上で2点間の距離を計算するには、複数の手法が存在します。前述した「球面三角法をそのまま適用」だと誤差が出ますので、Vincenty法や国土地理院が採用した方法など、より精度が高い複数の計算式が存在します。ただ、いずれも手で実装するには複雑で、バグが起きやすい箇所でもあります。
そのため、「日本国内で使える簡便な手法」と、「世界どこでも使える高精度な手法」をそれぞれ紹介します。
1. 簡便な手法
地球は真球ではなく楕円体とみなせる……といった話は先ほどしましたが、「1つの県」など比較的狭い範囲内では、平面とみなして概算できることがあります。市販されている地図は「平面」で、その上に定規を当てて「測量」した人はいるかと思いますが、それと近いイメージですね。
そのため日本では、「平面直角座標系」という方式が採用されています。これは日本列島を19の区画に分けたもので、同じ区域内であれば、
- その区域における直交座標を求める (緯度経度から変換しておく)
- 直交座標同士で、三平方の定理により距離を求める
だけで、2点間の距離を求めることができます。ただし、この方法は「日本国内」でのみ有効ですし、「緯度経度を直交座標に変換」部分がちょっとややこしいのでご注意ください。大量に変換する場合はライブラリを、そうでない場合は国土地理院提供のツールを使うと楽に行えます。
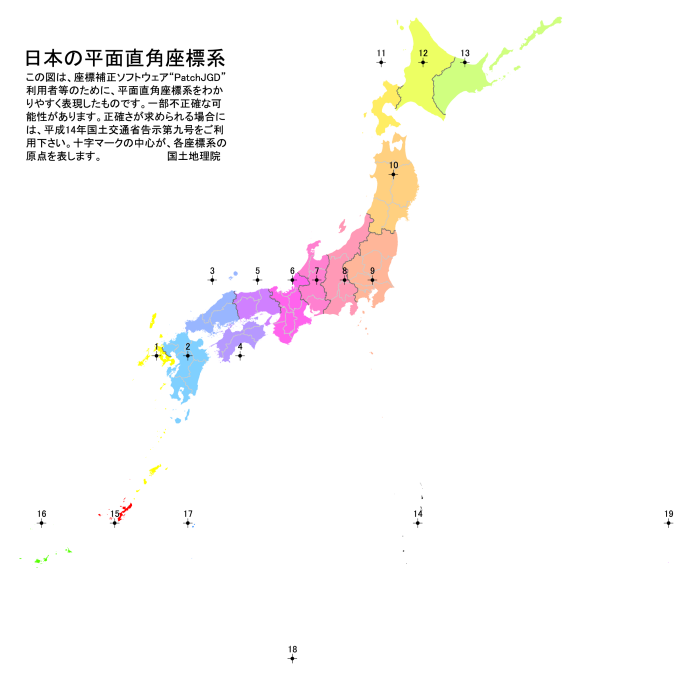
(出典:国土地理院ウェブサイトの説明ページ)
2. 精密な方法
そもそもプログラムで計算するので複雑な式でも問題ない、より一般的な計算式にしたい、といった場合は、より精密な計算式を使うとよいでしょう。その中でも、GeographicLib というライブラリは、特に高精度な計算を行えるそうです。
公式サイトではC++版と、各種言語への移植版を入手できます。PyPyやMavenやnpmなどのメジャーどころは抑えられてますので、導入も簡単です。
より高機能なライブラリとしては、pyprojというPython用ライブラリもあります。様々な地球楕円体や測地系などのパラメーターがライブラリ内で定義されていますので、複雑な計算を行う際も読みやすいかと思われます。
import math
import pyproj
# 各種座標系を読み込む
wgs84 = pyproj.Proj(init='EPSG:4326') # WGS84
rect7 = pyproj.Proj(init='EPSG:2449') # 平面直角座標系7系
grs80 = pyproj.Geod(ellps='GRS80') # GRS80楕円体
# 緯度・経度
lat1, lng1 = cnv(36, 8, 3.4), cnv(137, 14, 36.8) # 宮水神社
lat2, lng2 = cnv(35, 11, 7.77), cnv(136, 53, 56.71) # 名古屋城
# 直交座標
x1, y1 = pyproj.transform(wgs84, rect7, lng1, lat1)
x2, y2 = pyproj.transform(wgs84, rect7, lng2, lat2)
# 計算結果
print(f'精密に計算した距離:{grs80.inv(lng1, lat1, lng2, lat2)[2]}')
pythagorean = math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
print(f'三平方の定理を使った距離:{pythagorean}')
おまけ:国土地理院提供のREST APIについて
国土地理院提供の測量計算サイトでは、緯度経度と直交座標の変換、緯度経度間の距離・角度を計算、地殻変動に伴う座標補正計算など、様々なツールが提供されています。
ここで、それらの計算ツールはWebフォームとしての提供ですが、なんとREST APIとしても提供されています。利用規約への同意は必要で、「同一IPアドレスからのリクエストは、10秒間で10回」という制約は掛かるものの、複雑な計算を手軽に行えるという意味では有力な手段となります。
例えば、東京タワー (35.658711203641, 139.7454329037751)から通天閣(34.652722115220605, 135.5063427632938)までの距離を求める場合、以下のようなリクエストを送信します。
ENDPOINT="https://vldb.gsi.go.jp/sokuchi/surveycalc/surveycalc/bl2st_calc.pl"
OUTPUT_TYPE="json"
ELLIPSOID="GRS80"
LATITUDE1="35.658711203641"
LONGITUDE1="139.7454329037751"
LATITUDE2="34.652722115220605"
LONGITUDE2="135.5063427632938"
curl -X GET "${ENDPOINT}?outputType=${OUTPUT_TYPE}&ellipsoid=${ELLIPSOID}&latitude1=${LATITUDE1}&longitude1=${LONGITUDE1}&latitude2=${LATITUDE2}&longitude2=${LONGITUDE2}"
# 出力例 (本来は整形されてない結果が送られる)
# {
# "OutputData":{
# "geoLength":"402005.998",
# "azimuth1":"255.111033333333",
# "azimuth2":"72.6693194444445"
# }
# }
#
# つまり約 402km 離れていて、
# 方位角は出発点→到着点が約 255.1 度、
# 到着点→出発点が約 72.7 度
- 閲覧数 2139





コメントを追加